Equation horaires paramétriques et équation de la trajectoire

Compte tenus de notre niveau de connaissance (1ere s) , nous admettrons la propriété suivante :

Les vecteurs vitesse et accélération sont respectivement les dérivées et dérivées secondes du vecteur position 

et les coordonnées du  vecteur positions à une date t nous sont données par :

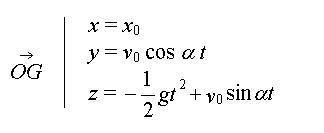
Donc en dérivant ce système nous obtenons les equations du vecteur vitesse :

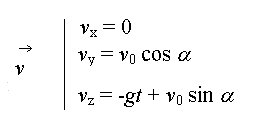
Puis en dérivant ce système nous obtenons donc les equations du vecteur accélération :

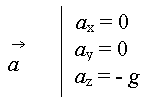
En éliminant le temps dans ces équations nous obtenons l'equation de la trajectoire (z en fonction de y) qui est :

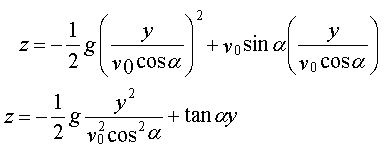
Nous remarquons donc bien que ici toutes les forces aérodynamiques sont donc bien négligés